Software Reliability
Return DfRSoft.com Home Page
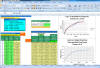
Software Reliability Growth Models -1) DfRSoft has multiple methods for assessing software reliability growth in testing. These can be viewed in two categories, 1) the well known Goel-Okumoto (G-O) Model, 2)Cumulative Reliability Growth Models. Each is described below:
Goel-Okumoto (G-O) Software Reliability Growth Model
Often it is observed that testing (and hence defect fixing) cycle gets elongated during product development. Manager is asked questions like, “How long will testing go on? How many defects are still remaining in software? How do we predict reliability of current software? At such time, it is better to use statistical methods to take informed decisions, rather than guessing with past experience. The method described here is based on Non-Homogeneous Poisson Process (NHPP) G-O model. It uses historical sample test data to predict how many residual defects are there in the software system and how many days are needed.
Cumulative Software Reliability Growth Models
DfRSoft offers a number of cumulative software reliability growth
models. These model are based on Cumulative Time vs. Cumulative Error
Data Fits. They include The Duane Model, Crow/AMSAA Model, The
Logarithmic Model, and a Polynomial Fit Model. Often the Logarithmic
model is the best chose. However, one should use the model that best
fits the data points and projected results. The key to remember is that
all the models are based on cumulative time rather than test time.
Therefore one should always keep this in mind in projecting model
results. Duane and Crow/AMSAAA are well known traditional reliability
growth models. They can also be used in software reliability growth. All
these models have advantages over the G-O model above. The max errors in
the G-O model is the value A. This limits the use of the model. These
models do not have this limit. They are more straight forward, being
basic regression and well understood. All models are based on data fits
of Cum Errors plotted against cumulative time. For the Duane and
Crow/AMSAA, the result is a power law fit to the data. Beta and
alpha=1-Beta are considered the growth exponent for these models.
![]()